Udæmpede svingninger
Vi ser på et lod ophængt i en fjeder. Vi trækker loddet ud fra ligevægtsstillingen (hvor det hænger i ro),
og lader det så, i første omgang udføre udæmpede svingninger. Den tilhørende differentialligning
opskrives samt den tilhørende bevægelsesligning.
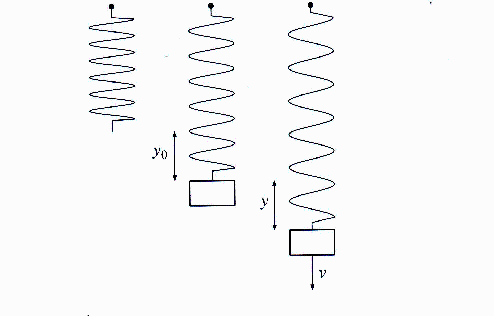
Vi ser på fjederen med en masse m, loddet. Fjederen er så let i forhold til massen m, at vi ser bort fra fjedermassen.
Bevægelsesligningen er
![]()
![]()
Med definitionen: ![]()
![]()
![]()
![]()
![]()
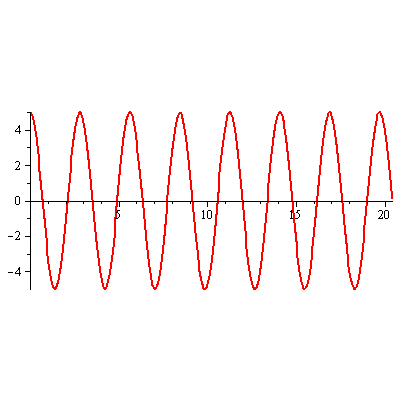
Denne oscillator vil bevæge sig uændret for evigt (se svingningsfunktionen herunder). Men det vil aldrig ske, for en virkelig oscillator.
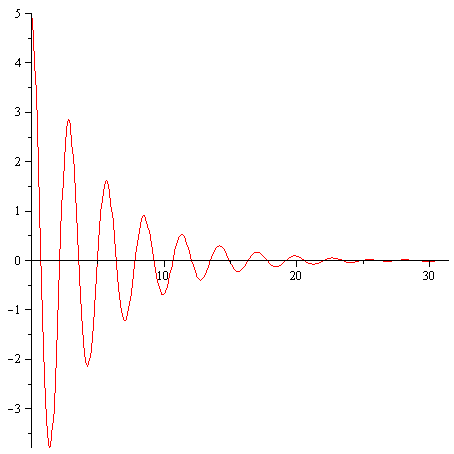
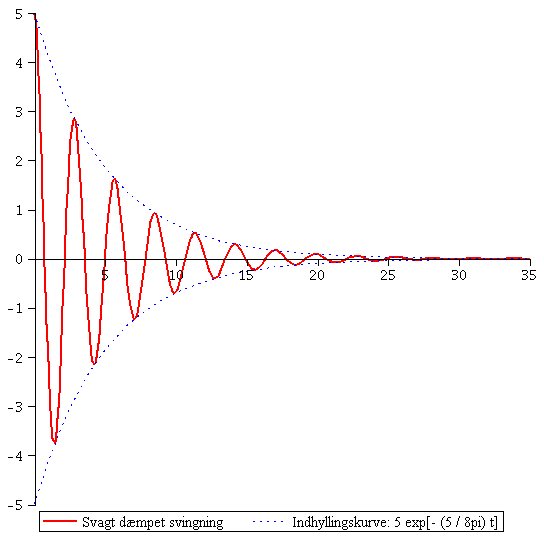
Friktion, i en eller anden form, vil altid optræde. Derved bremses svingningerne, og udsvinget bliver mindre og mindre som tiden går.
![y(t) = `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(gamma, `*`(t)))))), `*`([`+`(`*`(C, `*`(cos(`*`(sqrt(`+`(`*`(`^`(omega[0], 2)), `-`(`^`(`+`(`*`(`/`(1, 2), `*`(gamma))), 2)))), `*`(t))))), `*`(D, `*`(sin(`*`...](images/damp_oscillator_short2_15.gif)
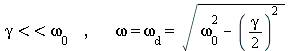
![y(t) = `*`(A, `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(gamma, `*`(t)))))), `*`(sin(`+`(`*`(omega[d], `*`(t)), `ϕ`)))))](images/damp_oscillator_short2_17.gif)
![y(t) = `*`(A, `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(gamma, `*`(t)))))), `*`(cos(`*`(omega[d], `*`(t))))))](images/damp_oscillator_short2_19.gif)