Dæmpede svingninger (svagt dæmpet harmonisk oscillator):
af john V. Petersen
Når en partikel bevæger sig påvirket af en elastisk kraft proportional med afstanden fra partiklen
til ligevægtspunktet kaldes den en harmonisk oscillator.
I dette eksempel vil vi se på dæmpede svingninger (dæmpet oscillator).
Eksempler på dæmpede oscillatorer er: Svingningerne i en kirkeklokke der ringer,
dæmpes af den omgivende luft. En oscillerende elektrisk ladning (en elektron),
der dæmpes, når den udsender elektromagnetisk stråling. F.eks. i en sender.
Eksemplet vi ser på:
Svagt dæmpet svingning af en masse (m) ophængt i en fjeder.
Dette eksempel er meget konkret og nemt at overskue. Og det giver de samme dæmpede
svingninger som et mere kompliceret eksempel.
For at starte med noget synligt, der kan vække interessen for at læse resten,
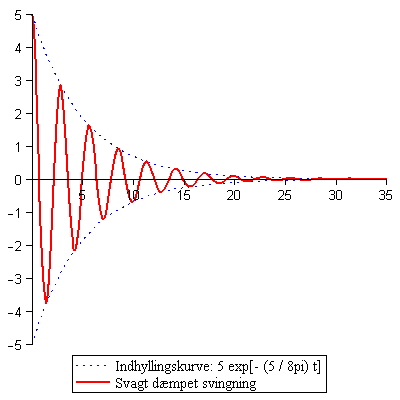
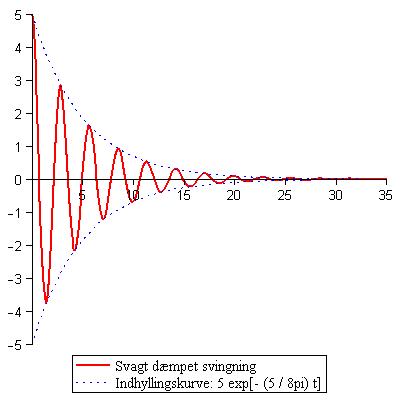
viser jeg herunder grafen for en svagt dæmpet svingning af en masse (m) ophængt i en fjeder.
Afbildningen viser amplituden (udsvinget fra hvilestilling) som funktion af tiden.
Du skal forstille dig, at loddet svinger op og ned ad y-aksen fra -5 til 5, med ligevægtspunkt ved y = 0.
(Bemærk, at det svarer til oscillationerne i kirkeklokken eller en oscillerende elektron som udsender
elektromagnetisk stråling.)
Grafen viser så udsvingets størrelse mens tiden går.
for 
med 
dvs. γ er dæmpningskonstanten pr. enhedsmasse (pr. kg)
ω er vinkelfrekvensen, t er tiden og ϕ er vinklen ved start (t=0).
-------------------------------------------------------------------------------------
| > |  |
| (1) |
| > |  |
 |
(2) |
| > |
| > |  |
 |
(3) |
| > |  |
 |
(4) |
| > |   |
| > |   |
| > |  |
| > |   |
 |
-------------------------------------------------------------------------------------------------------------------------
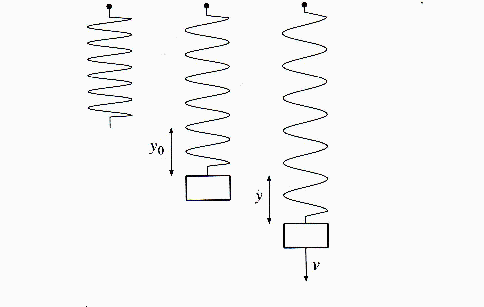
Nu starter vi helt forfra og ser på et lod ophængt i en fjeder. Vi trækker loddet ud fra
ligevægtsstillingen (hvor det hænger i ro), og lader det så udføre dæmpede sving-
ninger. Så ser vi på de kræfter der virker på loddet og opstiller derved den tilhørende
differentialligning, og finder den endelige bevægelsesligning, som er vist ovenfor.
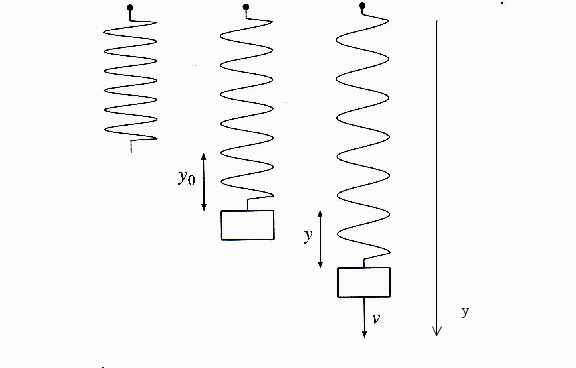
Vi ser på fjederen med en masse m, loddet. Fjederen er så let i forhold til massen m, at vi ser bort fra fjedermassen.
Vi ser først på systemet når det hænger i ro. 
(ifølge Hookes lov er fjederkraften lig med 
Vi har valgt positiv retning nedad. 
Vi kalder denne stilling for systemets ligevægtsstilling.
Nu trækker vi loddet længden y ud fra ligevægtsstillingen, og ladet systemet udføre harmoniske svingninger omkring 
Først ser vi på det idealiserede tilfælde, hvor oscillatoren vil bevæge sig for evigt ude at blive dæmpet. Dvs. vi ser bort fra friktion.
Dette vil aldrig ske for en virkelig oscillator.
Når fjederen er strakt længden y ud fra 
da 
for 
+ 
Karakterligningen til (2) er: 
og løsningen til (2) er så: 
Ved brug af additionsformlen for sinus, 
kan vi skrive løsningen på faseform:
Med løsningen 
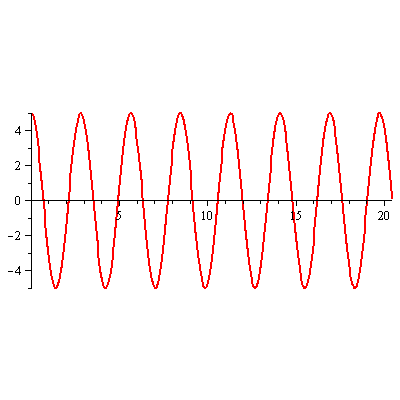
Vi plotter funktionen. Enheden på y-aksen er 
x-aksen 
| > |  |
| > |  |
| > |  |
 |
(5) |
| > |  |
 |
| > |
Du skal forstille dig, at loddet svinger op og ned ad y-aksen fra -5 til 5, med ligevægtspunkt ved y = 0.
Grafen viser så udsvingets størrelse mens tiden går.
Her vil systemet svinge som ovenfor til evig tid.
-------------------------------------------------------------------------------------------------------------------------
Nu ser på tilfældet hvor oscillatoren bliver dæmpet pga. friktion:
Vi antager, at friktionskraften er proportional med loddets hastighed v. Friktionskraften er så 
Denne proportionalitet vil gælde, tilnærmet, når en partikel bevæger sig i en væske eller i luften.
Summen af kræfterne på systemet er: 
Vi har tidligere set ( 1 ), at 
dvs. 
= 0 (4)
Vi bruger definitionerne, som vi kender fra tidligere: 
og får den homogene, lineære, anden ordens differentialligning med konstante koefficienter:
= 0 (5)
Karakterligningen har udseendet: 
med rødder 
eller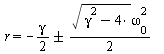 
arten af løsningerne bestemmes af udtrykket 
Ved dæmpede svingninger , 
med realdel 
imaginærdel 
Vi ser nu på det tilfælde, som specielt interesserer os nu: Svagt dæmpede svingninger
dvs. 
Nu kan vi igen skrive løsningen på faseform, som i (3)
ift. (3) 
har vi nu dæmpningsfaktoren 
Nu kan vi plotte funktionen:
Men først ser vi lige på de fysiske størrelser og de tilhørende enheder:
Fysiske størrelser og enheder
for 
---------------------------------------------------------------------------------------------------------------
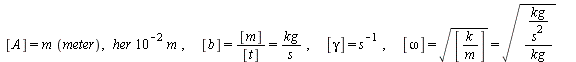
Plot af svingningsfunktionen for en svagt dæmpet oscillator
Konkret eksempel: 
Nu kan vi gentage plottet fra starten af dette dokument, med den forskel at vi nu har udledt bevægelsesligningen
| > |  |
| > |  |
| (6) |
| > |  |
 |
(7) |
| > |
| > |  |
 |
(8) |
| > |  |
 |
(9) |
| > |   |
| > |   |
| > |  |
| > |   |
for oscillatoren.
| > |
 |
| > |
I starten af dette dokument nævnte jeg et par eksempler på dæmpede oscillatorer.
Det ene eksempel nævnte svingningerne i en kirkeklokke der ringer. Her dæmpes svingningerne af den omgivende luft. Når en hammer slår hurtigt på en kirkeklokke, vil klokken begynde at ringe. Overfladen af klokken udfører harmoniske oscillationer med adskillige frekvenser, og, svingningerne bliver dæmpet, hovedsageligt pga. en kopling til den omgivende luft. Energien i klokkens svingninger bliver langsomt ændret til andre frihedsgrader, i lydbølger i den omgivende luft.
Klokken udsender lydbølger, som svarer til svingningernes frekvenser. Klokken vil ringe et stykke tid.
Det er en svagt dæmpet oscillator, med 
Man kan sige, at 
i dette tilfælde,
beskriver koblingen mellem klokkens oscillationer og lydfeltet i luften.